作者:刘康桥
近日,理学院青年教师刘康桥在物理与天体物理领域TOP期刊Communications Physics (中科院1区TOP,IF:5.4) 期刊发表题为“Dynamical activity universally bounds precision of response in Markovian nonequilibrium systems”的研究性论文。西华大学为该论文的第一完成单位。西华大学理学院刘康桥博士为该论文的第一作者与共同通讯作者,成都教育科学研究院古杰博士为论文的共同通讯作者。该研究发表后引发广泛关注,受Nature集团Nature Portfolio Communities的邀请,在“Behind the Paper”栏目撰稿分享研究经历。原文链接:https://doi.org/10.1038/s42005-025-01982-w

图1论文页面截图
热力学第二定律指出,孤立宏观系统的总熵随着时间的推移永远不会减少。然而,现实中大多数系统都受到显著的涨落和耗散的影响,因此它们通常处于非平衡状态,例如纳米机器或生化系统。在这种情况下,传统的平衡热力学框架变得不再适用。过去三十年来,随机热力学得到了极大的发展,为理解远离平衡状态下的耗散和热涨落提供了一个通用框架。
最近,在随机热力学框架中发现了一个严格的结果,称为热力学不确定性关系(TUR),它规定对于一个非平衡的马尔可夫跳跃过程,非平衡电流可观测量J(如热流或电荷流等)的精度下界受到由熵产生(EP)所表征的热力学耗散的限制。
然而,人们意识到,仅靠耗散可能不足以完全限制系统的涨落。对于远离平衡的系统,一个关键的非耗散度量是动力学活性(DA),它表示在随机过程中状态跃迁的频率,从而表征了系统的动力学。与TUR并行,已经证明流的精度也受到动力学不确定性关系(KUR)的限制。
与此同时,除了经典的涨落-耗散关系外,表征非平衡系统对外部扰动的静态响应的基本原理的研究也取得了丰硕的成果。图2展示了一个时间积分流在系统控制参数θ扰动下的示意图。值得注意的是,最近有人提出并证明了适用于非平衡稳态的时间无关马尔可夫跳跃过程的响应热力学不确定性关系(R-TUR)[K. Ptaszyński 等,Phys. Rev. Lett. 133, 227101 (2024)]。
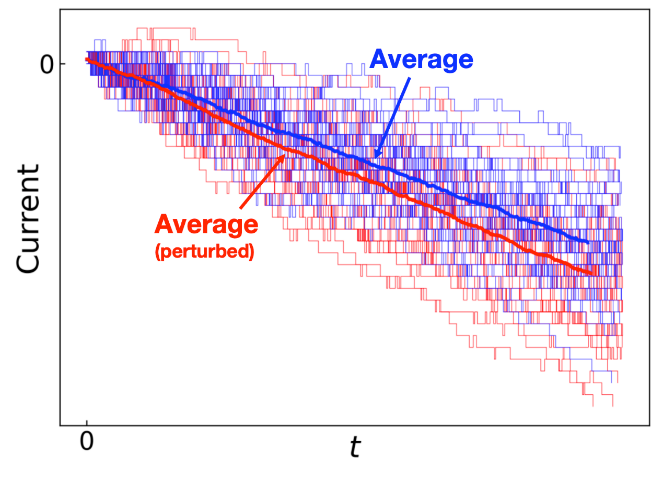
图2三态模型在时间t的弛豫过程中,时间积分流的蒙特卡罗模拟
一个自然而引人注目的问题随之而来:是否存在以动力学活性(DA)为基准的R-TUR对应物?换句话说,响应的精度与非平衡过程中的流量之间是否存在基本的关系?
我们通过建立严格的响应动力学不确定性关系(R-KUR)来回答上述问题——这是一种一般的可观测量对任意扰动的响应精度与动力学活性(DA)之间的权衡,它是R-TUR的补充但更为普适。它告诉我们,提高灵敏度和精度必然意味着更频繁的跃迁;或者,对于给定的随机动力学(固定的跃迁频率),对控制参数变化的高灵敏度意味着更大的涨落或更低的精度。
与仅适用于时间无关的马尔可夫过程稳态和流的R-TUR相比,我们的R-KUR可以应用于任意马尔可夫跳跃过程,并且不需要对驱动速度或观察时间进行扰动,使其在应用中更加通用。我们还注意到,R-KUR适用于任何可以用主方程描述的过程,而不限于热力学系统。
我们在两个例子中检验了我们的R-KUR。第一个例子是一维偏置随机游走,这是一个成功描述生物系统中分子马达动力学的模型,例如在细胞骨架微管上移动的驱动蛋白(如肌动蛋白)。我们通过扰动对称参数θ(这是验证R-TUR所必需的)或扰动反对称参数α(可能会破坏R-TUR)检验了界的效率,该效率应该受到1的上限限制。数值结果如图3所示。显然,我们的R-KUR始终成立,但R-TUR在扰动α时可能会被打破。令人鼓舞的是,带有α扰动的R-KUR在所有参数值下都达到了等式,而带有θ扰动的R-KUR在远离平衡状态下(以大耗散-活性比为特征)趋近等式。第二个例子请参阅我们的文章原文。
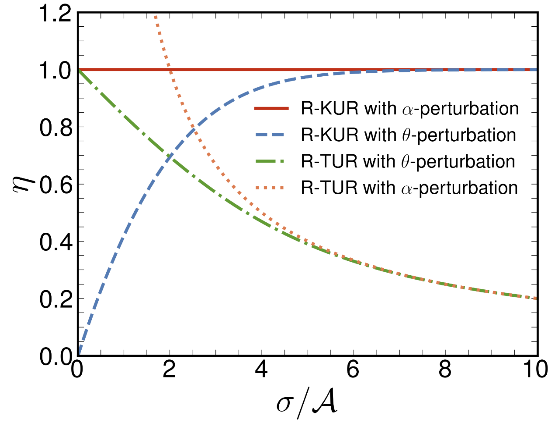
图3一维有偏随机行走者中,以耗散-活性比率作为函数的R-TURs和R-KURs的界效率η的数值模拟
我们的R-KUR的广泛适用性凸显了它在从生化过程(如生化传感、开关和分子马达)到远离平衡操作的工程纳米结构等多个领域的潜在应用。我们研究结果的一大特点是,所有相关量都可以通过随机跳跃的统计数据在实验中进行测量。值得一提的是,DA的测量有时比EP的测量更为容易,因为后者需要区分跃迁的方向。实验上可用于验证我们的结果的物理体系包括但不限于金刚石NV色心、低温下的单电子盒、分子马达、核磁共振(NMR)设置、纳米尺度电子导体以及超导NISQ量子处理器等。
作者简介

刘康桥,理学博士,讲师。2023年12月起任教于西华大学理学院,主要从事非平衡物理与深度学习算法的基础理论研究。已在国际学术期刊发表SCI论文3篇,国际会议发表论文3篇,总被引234次,H因子4。以第一/通讯作者在Physical Review Letters(IF = 9.185,中科院1区TOP)发表论文1篇,在Communications Physics(IF = 5.4,中科院1区TOP)发表论文1篇,在机器学习国际顶级会议ICML与ICLR发表论文各1篇。长期担任Physical Review Letters, Physical Review Research, Physical Review E等期刊与NeurIPS, ICLR, ICML等会议审稿人。

